Типы погрешностей
В методе обратного распространения точности приведены формулы для вычисления погрешностей сигналов сети. Эти формулы рассчитаны для сигналов, полученных при прямом функционировании сети с одним примером из обучающей выборки в качестве входных сигналов сети. Вообще говоря, допустимые погрешности сигналов зависят от вида входных сигналов сети. Исходя из этого, для метода обратного распространения точности можно выделить четыре типа допустимых погрешностей:
- погрешности, вычисленные для одного примера;
- погрешности, вычисленные для всей обучающей выборки;
- погрешности, вычисленные для примеров, компоненты которых принадлежат области , где
 - размерность области,
- размерность области, - действительные числа;
- действительные числа;
- погрешности, вычисленные для примеров, компоненты которых принадлежат области , где R - действительное число.

Погрешности первого типа вычисляются по формулам, описанным в методе обратного распространения точности.
Для того, чтобы вычислить погрешности второго типа, вычисляем погрешности для каждого примера из обучающей выборки. Затем в качестве допустимой погрешности для каждого элемента сети выбирается минимум допустимых погрешностей этого элемента, вычисленных для каждого примера из обучающей выборки.
Рассмотрим, как вычисляются допустимые погрешности третьего и четвертого типов. В формулах для вычисления допустимых погрешностей входной сигнал используется только у нелинейного преобразователя. Допустимые погрешности остальных элементов сети от входных сигналов не зависят. Поэтому для вычисления этих типов погрешностей следует выяснить, какие сигналы будут входными для нелинейных преобразователей, если входные сигналы сети принадлежат области, которая является прямоугольником или шаром.
Для начала рассмотрим допустимые погрешности третьего типа, то есть те допустимые погрешности элементов сети, которые получаются при входных сигналах, принадлежащих прямоугольной области. Нам известны интервалы, в которых изменяются входные сигналы сети. Требуется вычислить интервалы для входных сигналов каждого элемента сети.
Будем вычислять их следующим образом. При прохождении интервалов через сумматор концы интервалов соответствующих входов умножаются на веса синапсов

Таким образом вычисляются допустимые погрешности сигналов сети для прямоугольной области входных сигналов сети.
Рассмотрим пример, в котором будем вычислять погрешности третьего типа. Воспользуемся нейросетью, изображенной на рис. 6.9. Нейросеть имеет такие же веса синапсов, но входные сигналы принадлежат прямоугольной области:

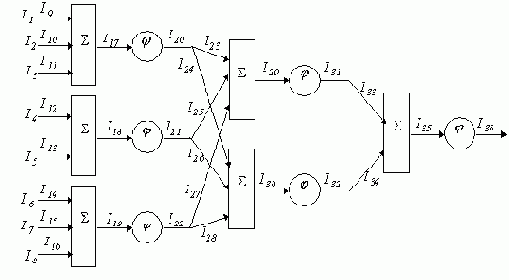
Рис. 6.12.
Сигналы сети изменяются в следующих интервалах:

Мы можем вычислить максимум производной функции активации на интервале изменения входного сигнала нелинейного преобразователя.






Зная эти величины, можно вычислить допустимые погрешности третьего типа.
Выясним теперь, как вычисляются допустимые погрешности сигналов четвертого типа, то есть погрешности, получающиеся, когда область входных сигналов сети является шаром.
Рассуждения, приведенные выше для допустимых погрешностей третьего типа, справедливы и для допустимых погрешностей четвертого типа. Отличие состоит в том, что нам необходимо "развернуть" шаровую область таким образом, чтобы получить интервалы, в которых изменяются входные сигналы элементов.
Рассмотрим для этого квадраты выходных сигналов сумматоров входного слоя сети. Используя неравенство Коши, получаем

где
