Метод обратного распространения точности для гарантированных интервальных оценок

Пусть нам заданы допустимые погрешности вычислений для выходных сигналов сети. Для каждого элемента решим задачу: определить допустимые погрешности на входах элемента по заданным максимально допустимым погрешностям на его выходе. Если эту задачу решить для каждого элемента сети, то можно оценить допустимые погрешности для всех сигналов, проходящих через сеть, переходя по сети от элемента к элементу в обратном направлении (от выходов сети к ее входам). Этот процесс мы назовем обратным распространением точности. В ходе него движение сигналов происходит от выходов ко входам, сигнал, проходящий по связи в обратном направлении, является допустимой погрешностью сигнала, проходящего по этой связи в прямом направлении.

Последним элементом стандартного нейрона является точка ветвления, поэтому начинаем рассмотрение метода обратного распространения точности именно с нее.

Точка ветвления имеет несколько выходов. Пусть для каждого ее выхода задана допустимая погрешность

(i - номер выхода). Для того, чтобы удовлетворить всем этим ограничениям погрешности, необходимо и достаточно, чтобы входной сигнал точки ветвления имел погрешность Таким образом, при обратном распространении точности тока ветвления заменяется на двойственный элемент, выбирающий из поступающих сигналов (т.е. погрешностей) минимальный.

Следующим элементом стандартного нейрона является нелинейный преобразователь. Пусть входной сигнал нелинейного преобразователя равен

, - его функция активации, - выходной сигнал и - допустимая погрешность выходного сигнала. Вычислим максимальную погрешность входного сигнала нелинейного преобразователя, то есть найдем отрезок такой, что для любого отличается от не более, чем на :

Ввиду непрерывности и дифференцируемости функции активации нелинейного преобразователя очевидно, что

, где

Пойдем традиционным путем, оценивая допустимую погрешность в линейном приближении:

По условию

Пользуясь этим неравенством, подберем

следующим образом: В этом случае формула для вычисления допустимой погрешности более простая, но менее точная.

Получили погрешность, допустимую для входного сигнала нелинейного преобразователя, которая одновременно является допустимой погрешностью для выходного сигнала сумматора. Аналогично можем вычислить погрешность входного сигнала нелинейного преобразователя любого стандартного нейрона, если известна погрешность его выходного сигнала.

Двойственный к нелинейному преобразователю элемент - просто линейная связь! Ее вес равен для линейного приближения в формуле ошибки или - в более общем случае (в последней формуле максимум берется по отрезку - так что линейность здесь уже кажущаяся).

Перейдем к следующему элементу стандартного нейрона - адаптивному сумматору с синапсами, являющимися его входами. Адаптивный сумматор - это сумматор, в котором входные сигналы суммируются с весами

Каждый вход сумматора имеет некоторую погрешность , которая вносит свой вклад в допустимую погрешность выходного сигнала сумматора. Эти погрешности могут иметь различные величины в зависимости от того, какой способ распределения допустимой погрешности выходного сигнала по входам сумматора мы выберем. Погрешности по входам сумматора могут распределяться равномерно, пропорционально и приоритетно.

Рассмотрим сначала равномерное распределение. Для этого полагаем, что на всех входах погрешности равны между собой Пусть - выходной сигнал сумматора без погрешностей. Тогда - множество выходных сигналов сумматора, получающихся, когда вектор входных сигналов сумматора пробегает вершины - мерного куба с центром в точке и ребром длины

где Нам требуется, чтобы все множество значений попало в интервал Для этого необходимо, чтобы



где максимум берется по всем Из этого неравенства и сделанного выше предположения о получаем требуемую оценку для равномерного распределения по входам сумматора:



При пропорциональном распределении погрешностей допустимая погрешность выходного сигнала сумматора делится сначала на число входов, а затем для каждого входа делится на соответствующий вес синапса. То есть погрешности распределяются пропорционально весам соответствующих синапсов.


Формула расчета допустимой погрешности для каждого входа сумматора имеет вид: , где - допустимая погрешность выходного сигнала сумматора, - число входов сумматора, - веса синапсов соответствующих входов сумматора.

При приоритетном распределении погрешностей сначала назначаются погрешности для тех входов, которые наиболее значимы по какому-либо признаку, а затем оставшуюся часть допустимой погрешности выходного сигнала сумматора распределяют между оставшимися входами равномерно или пропорционально.

Аналогично можно вычислить допустимые погрешности для входных сигналов сумматора любого стандартного нейрона, если известны погрешности для выходного сигнала сумматора.

Рассмотрим обученную нейросеть с вычисленными весами синапсов

Считаем, что погрешности входных сигналов, внутренних сигналов сети и элементов отсутствуют. При векторе входных сигналов получаем вектор выходных сигналов Вектор и внутренние сигналы сети будем считать точным вектором выходных сигналов и точными сигналами сети.

Рассмотрим теперь эту же сеть, но предположим, что все сигналы сети имеют некоторые погрешности. Пусть

- вектор выходных сигналов, полученный при том же векторе входных сигналов , но с погрешностями внутренних сигналов сети.

Предполагаем, что внутри каждого слоя погрешности сигналов

являются независимыми случайными величинами. Это предположение позволяет налагать менее жесткие требования при вычислении погрешностей сигналов.

Пусть нам задана

- допустимая погрешность выходных сигналов сети. То есть вектор может отличаться от вектора не более, чем на Будем считать величиной среднеквадратического отклонения выходных сигналов сети

Нам нужно выяснить, каким образом могут распределяться дисперсии сигналов при заданном

и вычислить среднеквадратические отклонения для всех сигналов сети такие, чтобы среднеквадратическое отклонение вектора выходных сигналов равнялось

Зная среднеквадратическое отклонение выходных сигналов, можем вычислить дисперсию выходных сигналов

, а затем, переходя от элемента к элементу в обратном порядке, вычислим дисперсии и среднеквадратические отклонения для всех сигналов сети.

Типичным участком сети является стандартный нейрон. Из стандартных нейронов состоит любая нейронная сеть. Поэтому нам достаточно определить, как вычисляются среднеквадратические отклонения сигналов для элементов стандартного нейрона. Тогда мы будем иметь возможность вычислить среднеквадратические отклонения для любого участка сети.

Выясним, как вычисляются среднеквадратические отклонения для входных сигналов точки ветвления, нелинейного преобразователя и сумматора, если нам будут известны среднеквадратические отклонения выходных сигналов этих элементов.

Если дисперсии выходных сигналов точки ветвления

при обратном распространении не равны между собой, то в качестве дисперсии входного сигнала точки ветвления выбирается

Пусть - среднеквадратическое отклонение погрешности выходного сигнала нелинейного преобразователя. Пусть случайная величина (погрешность входного сигнала нелинейного преобразователя) имеет некоторую плотность распределения Считаем, что математическое ожидание погрешности входного сигнала

и дисперсия



Пусть нелинейный преобразователь имеет функцию активации и точный входной сигнал Рассмотрим линейное приближение функции активации в точке Линейное приближение имеет вид:

Найдем математическое ожидание и дисперсию величины





С другой стороны, нам известно, что дисперсия выходного сигнала нелинейного преобразователя равна Отсюда получаем



Таким образом, мы вычислили среднеквадратическое отклонение входного сигнала нелинейного преобразователя для любого распределения погрешности входного сигнала

Мы получили среднеквадратическое отклонение входного сигнала нелинейного преобразователя , которое одновременно является среднеквадратическим отклонением выходного сигнала сумматора с погрешностями входных сигналов

Погрешность выходного сигнала сумматора равняется



где - точный выходной сигнал сумматора.

Вычислим среднеквадратические отклонения входных сигналов сумматора. Рассмотрим для этого дисперсию погрешности выходного сигнала сумматора

Предположим дополнительно, что равны между собой.



Получили формулу для равномерного распределения среднеквадратических отклонений по входам сумматора. Если в качестве погрешности каждого входа рассматривать не , а , то получим формулу для пропорционального распределения среднеквадратических отклонений по входам сумматора.





Получили погрешность, допустимую для входного сигнала нелинейного преобразователя, которая одновременно является допустимой погрешностью для выходного сигнала сумматора. Аналогично можем вычислить погрешность входного сигнала нелинейного преобразователя любого стандартного нейрона, если известна погрешность его выходного сигнала.

Двойственный к нелинейному преобразователю элемент - просто линейная связь! Ее вес равен для линейного приближения в формуле ошибки или - в более общем случае (в последней формуле максимум берется по отрезку - так что линейность здесь уже кажущаяся).

Перейдем к следующему элементу стандартного нейрона - адаптивному сумматору с синапсами, являющимися его входами. Адаптивный сумматор - это сумматор, в котором входные сигналы суммируются с весами

Каждый вход сумматора имеет некоторую погрешность , которая вносит свой вклад в допустимую погрешность выходного сигнала сумматора. Эти погрешности могут иметь различные величины в зависимости от того, какой способ распределения допустимой погрешности выходного сигнала по входам сумматора мы выберем. Погрешности по входам сумматора могут распределяться равномерно, пропорционально и приоритетно.

Рассмотрим сначала равномерное распределение. Для этого полагаем, что на всех входах погрешности равны между собой Пусть - выходной сигнал сумматора без погрешностей. Тогда - множество выходных сигналов сумматора, получающихся, когда вектор входных сигналов сумматора пробегает вершины - мерного куба с центром в точке и ребром длины

где Нам требуется, чтобы все множество значений попало в интервал Для этого необходимо, чтобы



где максимум берется по всем Из этого неравенства и сделанного выше предположения о получаем требуемую оценку для равномерного распределения по входам сумматора:



При пропорциональном распределении погрешностей допустимая погрешность выходного сигнала сумматора делится сначала на число входов, а затем для каждого входа делится на соответствующий вес синапса. То есть погрешности распределяются пропорционально весам соответствующих синапсов.


Формула расчета допустимой погрешности для каждого входа сумматора имеет вид: , где - допустимая погрешность выходного сигнала сумматора, - число входов сумматора, - веса синапсов соответствующих входов сумматора.

При приоритетном распределении погрешностей сначала назначаются погрешности для тех входов, которые наиболее значимы по какому-либо признаку, а затем оставшуюся часть допустимой погрешности выходного сигнала сумматора распределяют между оставшимися входами равномерно или пропорционально.

Аналогично можно вычислить допустимые погрешности для входных сигналов сумматора любого стандартного нейрона, если известны погрешности для выходного сигнала сумматора.

Для адаптивного сумматора можно вычислять как допустимые погрешности входных сигналов сумматора, так и допустимые погрешности весов синапсов. Для вычисления допустимых погрешностей весов синапсов также можно использовать равномерное, пропорциональное и приоритетное распределение погрешностей. При равномерном распределении допустимые погрешности для весов синапсов вычисляются по формуле:

где - входные сигналы сумматора.

При пропорциональном распределении допустимые погрешности для весов синапсов вычисляются по формуле: , где - число входов сумматора, - входные сигналы сумматора.

При приоритетном распределении сначала назначаются допустимые погрешности для тех весов синапсов, которые наиболее значимы по какому-либо признаку, а затем оставшуюся часть допустимой погрешности для выходного сигнала сумматора распределяют между оставшимися весами синапсов равномерно или пропорционально.

При обратном распространении точности имеет место специфическая двойственность - элементы сети заменяются на двойственные им. Однако, эта двойственность отличается от той, с которой мы встречаемся при изучении обратного распространения ошибки для вычисления градиентов функции оценки. Так, если в обычном обратном распространении двойственным элементом к точке ветвления является простой сумматор, то при обратном распространении точности вместо него, как было показано, появляется элемент, вычисляющий минимум приходящих на него сигналов.


Нелинейный преобразователь при обратном распространении точности заменяется двойственным ему элементом, умножающим сигнал на число. Но если при обратном распространении ошибки множителем является значение градиента, то в нашем случае сигнал умножается на величину обратную производной от входного сигнала нелинейного преобразователя. Адаптивный сумматор также заменяется двойственным ему элементом. Этот элемент является своеобразной точкой ветвления. Но, в отличии от простой точки ветвления, он сначала преобразует приходящий к нему сигнал в соответствии с выбранным распределением погрешностей по входам адаптивного сумматора, а затем передает полученные сигналы дальше.

Теперь мы знаем, каким образом вычислять гарантированную интервальную оценку погрешности для любого элемента стандартного нейрона методом обратного распространения точности.

1. Точка ветвления. Если допустимые погрешности выходных сигналов точки ветвления равны
   
   , то в качестве погрешности входного сигнала точки ветвления выбирается
   
   ( рис. 6.2).
   
   
   
   
   Рис. 6.2. 
   
   
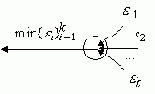
2. Нелинейный преобразователь. Пусть при прямом функционировании входной сигнал нелинейного преобразователя равен
   
   , его выходной сигнал равен
   
   и нелинейный преобразователь имеет функцию активации
   
   Если допустимая погрешность выходного сигнала нелинейного преобразователя равняется
   
   , то погрешность его входного сигнала не должна превышать
   
   , где
   
   или в линейном приближении
   
   ( рис. 6.3).
   
   
   
   
   Рис. 6.3. 
   
   
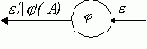
3. Адаптивный сумматор. Если при обратном распространении допустимая погрешность выходного сигнала адаптивного сумматора равняется
   
   , то погрешность каждого входа сумматора не должна превышать
   
   , где
   
   для равномерного распределения и
   
   для пропорционального распределения ( рис. 6.4).
   
   
   
   
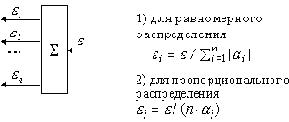
   Рис. 6.4. 
   
   

Зная, как вычисляются допустимые погрешности для всех элементов стандартного нейрона, можно вычислить допустимые погрешности сигналов для всей сети. Рассмотрим участок сети, состоящий из сумматора и нелинейного преобразователя, результатом работы которого является выходной сигнал , а также из сумматоров и нелинейных преобразователей, выходные сигналы которых являются входными сигналами сумматора (рис. 6.5).


То есть мы рассматриваем два последних слоя нейронной сети, состоящие из стандартных нейронов.


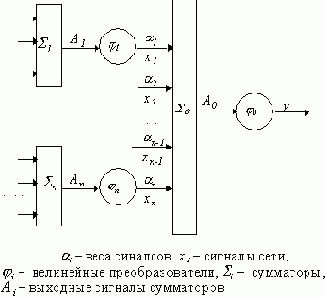
Рис. 6.5. 

Если заданы допустимые погрешности для выходных сигналов сети, можно вычислить допустимые погрешности для последнего слоя сети. Когда вычислены допустимые погрешности всех входных сигналов последнего слоя сети, переходим к вычислению допустимых погрешностей предпоследнего слоя и так далее. Переходя по сети в обратном направлении от слоя к слою, мы можем вычислить допустимые погрешности всех сигналов сети, в том числе допустимые погрешности входных сигналов.

Мы рассмотрели, как изменяются погрешности сигналов при прохождении через элементы сети. Предположим теперь, что не только сигналы имеют погрешности, но и все элементы сети передают приходящие к ним сигналы с некоторыми погрешностями. Пусть собственные погрешности элементов известны и фиксированы. Выясним, как влияют собственные погрешности элементов на погрешности сигналов.

Bыясним, как действуют элементы сети, имеющие собственные погрешности, при прямой работе сети.

Точка ветвления может либо вообще не иметь погрешности, либо она имеет собственную погрешность В последнем случае сигнал при прохождении через точку ветвления будет изменяться, оставаясь в интервале ( рис. 6.6).


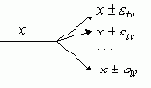
Рис. 6.6. 

Предположим, что сумматор имеет собственную погрешность Тогда возможны следующие варианты:

1. погрешность прибавляется к выходному сигналу сумматора, т.е. при прохождении сигналов
   
   через сумматор выходной сигнал сумматора будет иметь вид:
   
2. погрешность сумматора действует по каждому входу пропорционально
   
   ( рис. 6.7).

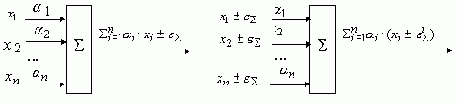
Рис. 6.7. 

Считаем при этом, что погрешности равны между собой и равны , где - число входов сумматора.

Пусть собственная погрешность нелинейного преобразователя равна , - входной сигнал нелинейного преобразователя, - его функция активации. Собственная погрешность может добавляться или к входному сигналу : , или к выходному сигналу нелинейного преобразователя: ( рис. 6.8).


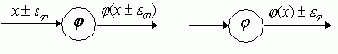
Рис. 6.8. 

Мы выяснили как вычисляются допустимые погрешности сигналов сети.


При этом мы не выделяли особо тот вклад, который вносят в погрешность сигнала сами элементы. Рассмотрим теперь, как вычисляются допустимые погрешности сигналов сети при обратном распространении точности с учетом собственных погрешностей элементов стандартного нейрона.

Начнем вычисление допустимых погрешностей сигналов сети с учетом собственных погрешностей элементов с точки ветвления. Пусть точка ветвления имеет собственную погрешность Предположим, что допустимые погрешности выходных сигналов точки ветвления равны Для увеличения точности вычислений необходимо накладывать на допустимые погрешности наиболее жесткие требования. Поэтому в качестве допустимой погрешности входного сигнала точки ветвления при обратном распространении следует выбирать погрешность

Следующий элемент стандартного нейрона - нелинейный преобразователь. Если нелинейный преобразователь имеет собственную погрешность , которая добавляется к его выходному сигналу, и погрешность его выходного сигнала равняется , то допустимая погрешность входного сигнала нелинейного преобразователя равняется , где

или в линейном приближении

Предположим теперь, что собственная погрешность нелинейного преобразователя добавляется к его входному сигналу , и при обратном распространении точности погрешность выходного сигнала нелинейного преобразователя равняется Рассмотрим наихудший вариант, когда входной сигнал нелинейного преобразователя находится в интервале

В этом случае допустимая погрешность входного сигнала нелинейного преобразователя вычисляется следующим образом:



где

Рассмотрим допустимую погрешность в линейном приближении:



По условию



Получаем:

или



И, наконец, перейдем к вычислению допустимых погрешностей входных сигналов сумматора. Рассмотрим вариант, при котором собственная погрешность сумматора добавляется к его выходному сигналу, и допустимая погрешность выходного сигнала сумматора равняется При обратном распространении точности получаем, что равномерно, пропорционально и приоритетно по выше полученным формулам распределяется погрешность



Если же собственная погрешность сумматора пропорционально распределяется по его входам, и допустимая погрешность выходного сигнала сумматора равняется , то допустимые погрешности для входов сумматора вычисляются следующим образом. Пусть - выходной сигнал сумматора без погрешностей. Тогда - выходные сигналы сумматора с учетом собственных погрешностей сумматора и погрешностей входных сигналов :



где Для того, чтобы все множество попало в интервал

необходимо, чтобы



где максимум берется по всем Из этого неравенства, предполагая что равны между собой, получаем требуемую оценку для :



Мы получили формулы для вычисления допустимых погрешностей сигналов для любого участка сети с учетом того, что все элементы имеют собственные погрешности, которые вносят свой вклад в погрешность выходного сигнала этих элементов.



Пусть - среднеквадратическое отклонение погрешности выходного сигнала нелинейного преобразователя. Пусть случайная величина (погрешность входного сигнала нелинейного преобразователя) имеет некоторую плотность распределения Считаем, что математическое ожидание погрешности входного сигнала

и дисперсия



Пусть нелинейный преобразователь имеет функцию активации и точный входной сигнал Рассмотрим линейное приближение функции активации в точке Линейное приближение имеет вид:

Найдем математическое ожидание и дисперсию величины





С другой стороны, нам известно, что дисперсия выходного сигнала нелинейного преобразователя равна Отсюда получаем



Таким образом, мы вычислили среднеквадратическое отклонение входного сигнала нелинейного преобразователя для любого распределения погрешности входного сигнала

Мы получили среднеквадратическое отклонение входного сигнала нелинейного преобразователя , которое одновременно является среднеквадратическим отклонением выходного сигнала сумматора с погрешностями входных сигналов

Погрешность выходного сигнала сумматора равняется



где - точный выходной сигнал сумматора.

Вычислим среднеквадратические отклонения входных сигналов сумматора. Рассмотрим для этого дисперсию погрешности выходного сигнала сумматора

Предположим дополнительно, что равны между собой.



Получили формулу для равномерного распределения среднеквадратических отклонений по входам сумматора. Если в качестве погрешности каждого входа рассматривать не , а , то получим формулу для пропорционального распределения среднеквадратических отклонений по входам сумматора.



Кроме равномерного и пропорционального распределения среднеквадратических отклонений погрешностей по входам сумматора, может быть использовано приоритетное распределение среднеквадратических отклонений. При этом сначала назначаются среднеквадратические отклонения погрешностей для тех входов сумматора, которые наиболее значимы по какому-либо признаку, а затем оставшаяся часть среднеквадратического отклонения погрешности выходного сигнала сумматора распределяется по остальным входам равномерно или пропорционально.



Мы рассмотрели, как изменяются погрешности сигналов при прохождении через элементы сети. Предположим теперь, что не только сигналы имеют погрешности, но и все элементы сети передают приходящие к ним сигналы с некоторыми погрешностями. Пусть среднеквадратические отклонения погрешностей элементов известны и фиксированы. Выясним, как влияют собственные погрешности элементов на погрешности сигналов.

Вычислим среднеквадратические отклонения входных сигналов точки ветвления, нелинейного преобразователя и сумматора, если известны среднеквадратические отклонения выходных сигналов и собственные погрешности этих элементов.

Пусть точка ветвления имеет собственную погрешность и среднеквадратическое отклонение собственной погрешности равно Собственная погрешность добавляется к каждому сигналу, выходящему из точки ветвления.

Если при обратном распространении получаем дисперсии выходных сигналов точки ветвления не равные между собой, то в качестве дисперсии входного сигнала точки ветвления, с учетом собственной погрешности, выбирается

Пусть среднеквадратическое отклонение собственной погрешности нелинейного преобразователя равно , а среднеквадратическое отклонение выходного сигнала нелинейного преобразователя равно Собственная погрешность нелинейного преобразователя может добавляться либо к результату работы нелинейного преобразователя: , либо к входному сигналу нелинейного преобразователя:

Рассмотрим оба варианта.

Пусть погрешность добавляется к результату работы нелинейного преобразователя. Рассмотрим дисперсию



Отсюда получаем, что дисперсия непосредственно выходного сигнала нелинейного преобразователя равна

Среднеквадратическое отклонение для входного сигнала нелинейного преобразователя вычисляется как указано выше. В качестве дисперсии выходного сигнала в формуле используется вычисленная дисперсия Среднеквадратическое отклонение погрешности входного сигнала нелинейного преобразователя будет равняться

Пусть теперь собственная погрешность нелинейного преобразователя добавляется к его входному сигналу: В этом случае погрешность входного сигнала имеет математическое ожидание





и дисперсию



Вычислим математическое ожидание и дисперсию выходного сигнала нелинейного преобразователя, рассматривая линейное приближение





Отсюда получаем

Перейдем к вычислению среднеквадратических отклонений входных сигналов сумматора. Пусть среднеквадратическое отклонение выходного сигнала сумматора равно , собственное среднеквадратическое отклонение погрешности сумматора равно

Собственная погрешность сумматора может добавляться либо к выходному сигналу сумматора:

либо к каждому входу сумматора:



где

Пусть собственная погрешность добавляется к выходному сигналу сумматора. Вычислим среднеквадратическое отклонение погрешностей для входных сигналов сумматора. Рассмотрим для этого дисперсию



Для равномерного распределения среднеквадратических отклонений предполагаем, что равны между собой.



Если будем рассматривать пропорциональное распределение среднеквадратических отклонений входных сигналов сумматора, то получим



Пусть теперь собственное среднеквадратическое отклонение сумматора добавляется к каждому входу сумматора:

Вычислим среднеквадратическое отклонение погрешностей для входных сигналов сумматора. Рассмотрим для этого дисперсию

Для равномерного распределения среднеквадратических отклонений предполагаем, что равны между собой.



Если будем рассматривать пропорциональное распределение среднеквадратических отклонений входных сигналов сумматора, то получим

Зная, как вычисляются среднеквадратические отклонения погрешностей для всех элементов стандартного нейрона, можно вычислить среднеквадратические отклонения погрешностей сигналов для всей сети. Если заданы среднеквадратические отклонения погрешностей для выходных сигналов сети, можно вычислить среднеквадратические отклонения погрешностей для последнего слоя сети. Когда вычислены среднеквадратические отклонения погрешностей всех входных сигналов последнего слоя сети, переходим к вычислению среднеквадратических отклонений погрешностей предпоследнего слоя и так далее.

Рассмотрим пример на рис. 6.10. Пусть дана сеть с тремя нейронами входного слоя, двумя нейронами скрытого слоя и одним выходным нейроном.


На рисунке показаны сигналы, проходящие по сети при данном векторе входных сигналов, и веса связей. В данном примере элементы сети не имеют собственных погрешностей. Характеристическая функция нелинейных преобразователей имеет вид: , где - входной сигнал нелинейного преобразователя. Среднеквадратическое отклонение вектора выходных сигналов сети равняется 0.01. Среднеквадратические отклонения погрешностей по входам сумматора вычисляются с использованием формулы для равномерного распределения среднеквадратических отклонений.


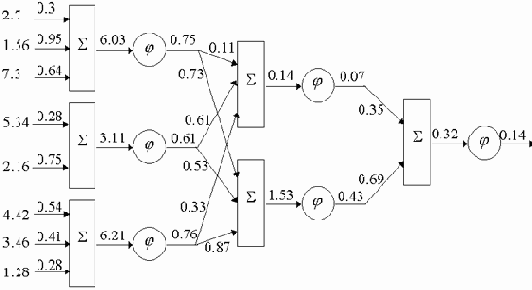
Рис. 6.10. 

Вычислим среднеквадратические отклонения для всех сигналов сети при данном векторе входных сигналов. Все вычисленные значения в этом примере округляются до двух знаков после запятой. На рис. 6.11 показаны вычисленные среднеквадратические отклонения для данного примера.


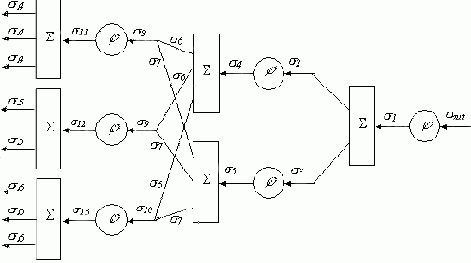
Рис. 6.11. 



























Таким образом, получены формулы для вычисления среднеквадратических отклонений погрешностей сигналов сети, в предположении, что погрешности являются независимыми случайными величинами.


Содержание раздела

---

---

---

Главная сайта

---