Возможности регуляризации обратной задачи
Займемся теперь рассмотрением обратной и комбинированной задач. Как мы уже убедились на основе расчетов, эти задачи обладают ярко выраженной некорректностью, связанной с неустранимой неоднозначностью обратной функции, поэтому интерес представляет возможность лишь их частичной регуляризации.
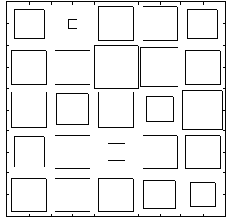
Рис. 4.11. Распределение ошибок обучения по кластерам карты Кохонена. Ошибка на данных каждого кластера пропорциональна размеру соответствующего квадрата.
Для исследований была выбрана комбинированная задача определения диаметра пламени по остальным параметрам пожара и измерениям внутри контейнера. Эта задача имеет минимальную ошибку обучения (22%) при использовании данных из всей области параметров. Для данной задачи был выполнен кластерный анализ на основе сети встречного распространения. Слой Кохонена представлял собой карту из 5x5=25 нейронов. рис. 4.11 отражает распределение ошибки обучения сети по кластерам карты, определяемым нейронами Кохонена.
Результирующее распределение ошибок близко к равномерному, однако имеются две области (кластеры 1-2 и 4-3 в матричных обозначениях) с относительно малыми ошибками. Эти кластеры определяют области частичной регулярности задачи в 7-мерном пространстве параметров.
Наиболее регулярной является область кластера 1-2. Анализ значений параметров, отвечающих центроиду данного кластера, позволяет заключить, что наименьшая ошибка определения диаметра пламени путем решения обратной задачи достигается для высокотемпературных (около 1000oC), длительных (более получаса) пожаров при промежуточных расстояниях до эпицентра (масштаба диаметра пламени).
Следующий шаг исследований состоял в классификации записей в базе данных по построенным кластерам обученной сети Кохонена. Из полного набора измерений около 2.5% данных оказалось относящимися к наиболее регулярному кластеру 1-2. Эти данные были использованы для обучения многослойной сети с обратным распространением с 7 входами и одним выходом.
Результирующая ошибка регуляризованного решения составила лишь 8.5%, что приблизительно в три раза меньше ошибки обучения на полном наборе векторов.
Результаты описанных исследований могут быть обобщены в нейросетевую технологию решения обратных и комбинированных задач:
- Для данной комбинированной задачи оценивается степень ее некорректности по ошибке обучения нейронной сети с обратным распространением, использующей известные параметры в качестве входов, а запрашиваемые параметры в качестве оцениваемых выходов.
- Если указанная ошибка мала (имеется сходимость нейросетевой аппроксимации), то построенная нейросеть дает искомое решение. Следует далее оценить ошибку обобщения, исходя из априорных теоретических соображений о сложности нейросети, или на основе прямых вычислений с использованием тестовых данных. При недостаточном качестве обобщения можно попытаться уменьшить число нейронов в скрытых слоях нейросети и применить алгоритмы удаления наименее значимых связей.
- В случае неприемлемо больших ошибок обучения применяется уже описанная технология дифференциальной оценки степени некорректности задачи. После кластерного анализа данных на основе сети Кохонена16) оценивается распределение ошибок обучения в пространстве параметров модели. Далее строится система малых экспертов, использующих данных отдельных кластеров, или строится более укрупненная оценка на основе сети встречного распространения.
Промышленная нейросетевая модель, созданная по данной технологии будет содержать материнскую сеть Кохонена и семейство малых сетей-экспертов с обратным распространением ошибки. Такая системная модель предоставляет пользователю
- семейство решений для прямых задач
- регуляризованное решение обратных и комбинированных некорректно поставленных задач с оценкой точности, в областях значений параметров с малой локальной степенью некорректности задачи, либо
- диагностическое сообщение о невозможности уверенного прогноза вследствие принадлежности вектора пользовательского запроса области сильной неустранимой нерегулярности задачи.
Предлагаемый подход к нейросетевому моделированию сложных технических систем относительно прост в реализации и непосредственно соответствует ежедневным информационным потребностям инженеров, связанных с эксплуатацией таких систем.