Нейронные сети в информационном моделировании

Искусственные нейронные сети (ИНС) являются удобным и естественным базисом для представления информационных моделей. Нейросеть может быть достаточно формально определена [4.3], как совокупность простых процессорных элементов (часто называемых нейронами), обладающих полностью локальным функционированием, и объединенных однонаправленными связями (называемыми синапсами ). Сеть принимает некоторый входной сигнал1) из внешнего мира, и пропускает его сквозь себя с преобразованиями в каждом процессорном элементе. Таким образом, в процессе прохождения сигнала по связям сети происходит его обработка, результатом которой является определенный выходной сигнал. В укрупненном виде ИНС выполняет функциональное соответствие между входом и выходом, и может служить информационной моделью G системы F.

Определяемая нейросетью функция может быть произвольной при легко выполнимых требованиях к структурной сложности сети и наличии нелинейности в переходных функциях нейронов [4.4]. Возможность представления любой системной функции F с наперед заданной точностью определяет нейросеть, как компьютер общего назначения. Этот компьютер, в сравнении с машиной фон Неймана, имеет принципиально другой способ организации вычислительного процесса - он не программируется с использованием явных правил и кодов в соответствии с заданным алгоритмом, а обучается посредством целевой адаптации синаптических связей (и, реже, их структурной модификацией и изменением переходных функций нейронов) для представления требуемой функции.

В гипотетической ситуации, когда функция системы F известна или известен алгоритм ее вычисления при произвольных значениях аргументов, машина фон Неймана наилучшим средством для моделирования (состоящего в вычислении F), и необходимость в информационных моделях отпадает.

При моделировании реальных сложных технических систем значения системной функции F получаются на основе экспериментов или наблюдений, которые проводятся лишь для конечного параметров X. При этом значения как Y так и Х измеряются приближенно, и подвержены ошибкам различной природы (см.
Одним из новых эффективных применений сети Кохонена является построение тематической карты электронных сообщений в глобальных компьютерных сетях. При помощи такой карты пользователь получает возможность свободной навигации в бесконечном потоке сообщений, в соответствии с индивидуальным кругом интересов3). В применении к моделированию технических систем, карты Кохонена могут использоваться для выявления различий в режимах поведения системы, при этом могут выявляться аномальные режимы. Важно, что при этом могут быть обнаружены неожиданные скопления близких данных, последующая интерпретация которых пользователем может привести к получению нового знания об исследуемой системе.

Вторая группа технических применений связана с предобработкой данных. Карта Кохонена группирует близкие входные сигналы X, а требуемая функция Y=G(X) строится на основе применения обычной нейросети прямого распространения (например, многослойного персептрона или линейной звезды Гроссберга) к выходам нейронов Кохонена. Такая гибридная архитектура была предложена Р. Хехт-Нильсеном [4.7, 4.8], она получила название сети встречного распространения. Нейроны слоя Кохонена обучаются без учителя, на основе самоорганизации, а нейроны распознающих слоев адаптируются с учителем итерационными методами. При использовании линейных выходных нейронов значения их весов могут быть получены безитерационно, непосредственным вычислением псевдо-обратной матрицы по Муру-Пенроузу.

Сеть встречного распространения дает кусочно-постоянное представление модели Y=G(X), поскольку при вариации вектора X в пределах одного кластера на слое соревнующихся нейронов Кохонена возбуждается один и тот же нейрон-победитель. В случае сильно зашумленных данных, такое представление обладает хорошими регуляризирующими свойствами. При этом процедура обучения сети встречного распространения заметно быстрее, чем, например, обучение многослойного персептрона стандартным методом обратного распространения ошибок [4.9].

Другой альтернативой традиционным многослойным моделям является переход к нейросетям простой структуры, но с усложненными процессорными элементами.

В частности, можно рассмотреть нейроны высоких порядков, активирующим сигналом для которых является взвешенная сумма входов, их попарных произведений, произведений троек и т.д., вплоть до порядка k.

Каждый процессорный элемент k-го порядка способен выполнить не только линейное разделение областей в пространстве входов, но также и произвольное разделение, задаваемое поли-линейной функцией нескольких аргументов. Семейство решающих правил, определяемых нелинейным нейроном значительно богаче, чем множество линейно разделимых функций. На рис. 4.1 приведен пример решающего правила, задаваемого одним нейроном второго порядка, для классической линейно неразделимой задачи " исключающее ИЛИ ".

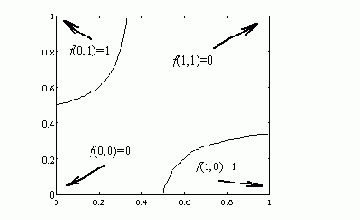
Рис. 4.1. Решающее правило для задачи "исключающее ИЛИ".

Важным достоинством нейронов высокого порядка является возможность строить нейросетевые модели без скрытых слоев, воспроизводящие широкий класс функций4). Такие нейроархитектуры не требуют длительного итерационного обучения, оптимальные веса даются решением уравнений регрессии. Другой отличительной чертой является возможность эффективной аппаратной (электронной или оптической) реализации корреляций высокого порядка. Так, например, существуют нелинейные среды, оптические свойства которых определяются полиномиальной зависимостью от амплитуды электрического поля световой волны. Потенциально, устройства, основанные на таких средах, могут обеспечить высокие скорости вычислений со свойственной оптическим компьютерам супер-параллельностью вычислений.

В этой леции описанные и другие нейроархитектуры будут применены к модельным и реалистичным задачам информационного моделирования сложных инженерных систем.

ниже). Целью моделирования является получение значений системных откликов при произвольном изменении X. В этой ситуации может быть успешно применена информационная (статистическая) модель G исследуемой системы F.

Информационные модели могут строиться на основе традиционных методов непараметрической статистики Данная наука позволяет строить обоснованные модели систем в случае большого набора экспериментальных данных (достаточного для доказательства статистических гипотез о характере распределения) и при относительно равномерном их распределении в пространстве параметров. Однако при высокой стоимости экспериментальных данных, или невозможности получения достаточного их количества (как, например, при построении моделей тяжелых производственных аварий, пожаров и т.п.), их высокой зашумленности, неполноте и противоречивости, нейронные модели оказываются более предпочтительными. Нейронная сеть оказывается избирательно чувствительной в областях скопления данных, и дает гладкую интерполяцию в остальных областях.

Эта особенность нейросетевых моделей основывается на более общем принципе - адаптивной кластеризации данных. Одной из первых сетей, обладающих свойствами адаптивной кластеризации была карта самоорганизации Т. Кохонена [4.5, 4.6]. Задачей нейросети Кохонена является автоматизированное построение отображения набора входных векторов высокой размерности в карту кластеров меньшей размерности, причем, таким образом что близким кластерам на карте отвечают близкие друг к другу входные вектора в исходном пространстве. Таким образом, при значительном уменьшении размерности пространства сохраняется топологический порядок расположения данных. При замене всех векторов каждого кластера его центроидом достигается высокая степень сжатия информации при сохранении ее структуры в целом4).

Карты Кохонена применяются в основном, для двух целей. Первая из них - наглядное упорядочивание многопараметрической информации. На практике обычно используются одномерные и двумерные карты. Кластеры, задаваемые узлами карты, содержат группы в некотором смысле похожих наблюдений, которым может быть приписан групповой семантический смысл.

Одним из новых эффективных применений сети Кохонена является построение тематической карты электронных сообщений в глобальных компьютерных сетях. При помощи такой карты пользователь получает возможность свободной навигации в бесконечном потоке сообщений, в соответствии с индивидуальным кругом интересов5). В применении к моделированию технических систем, карты Кохонена могут использоваться для выявления различий в режимах поведения системы, при этом могут выявляться аномальные режимы. Важно, что при этом могут быть обнаружены неожиданные скопления близких данных, последующая интерпретация которых пользователем может привести к получению нового знания об исследуемой системе.

Вторая группа технических применений связана с предобработкой данных. Карта Кохонена группирует близкие входные сигналы X, а требуемая функция Y=G(X) строится на основе применения обычной нейросети прямого распространения (например, многослойного персептрона или линейной звезды Гроссберга) к выходам нейронов Кохонена. Такая гибридная архитектура была предложена Р. Хехт-Нильсеном [4.7, 4.8], она получила название сети встречного распространения. Нейроны слоя Кохонена обучаются без учителя, на основе самоорганизации, а нейроны распознающих слоев адаптируются с учителем итерационными методами. При использовании линейных выходных нейронов значения их весов могут быть получены безитерационно, непосредственным вычислением псевдо-обратной матрицы по Муру-Пенроузу.

Сеть встречного распространения дает кусочно-постоянное представление модели Y=G(X), поскольку при вариации вектора X в пределах одного кластера на слое соревнующихся нейронов Кохонена возбуждается один и тот же нейрон-победитель. В случае сильно зашумленных данных, такое представление обладает хорошими регуляризирующими свойствами. При этом процедура обучения сети встречного распространения заметно быстрее, чем, например, обучение многослойного персептрона стандартным методом обратного распространения ошибок [4.9].

Другой альтернативой традиционным многослойным моделям является переход к нейросетям простой структуры, но с усложненными процессорными элементами.

В частности, можно рассмотреть нейроны высоких порядков, активирующим сигналом для которых является взвешенная сумма входов, их попарных произведений, произведений троек и т.д., вплоть до порядка k.