Граф вычисления сложной функции

Сложная функция задается с помощью суперпозиции некоторого набора "простых". Простые функции принадлежат исходно задаваемому конечному множеству F. Формально они выделены только принадлежностью к множеству F - никаких обязательных иных отличий этих функций от всех прочих в общем случае не предполагается.

В этом разделе мы изучим способы задания сложных функций, то есть формулы и соответствующие им графы. Свойства самих функций нас сейчас не интересуют (будем рассматривать ноты, а не слушать музыку).

Теория выражений, определяющих сложные функции, является простейшим разделом математической логики, в которой сами эти выражения называются термами [3.4].

Термы - это правильно построенные выражения в некотором формальном языке. Чтобы задать такой язык, необходимо определить его алфавит. Он состоит из трех множеств символов:

1. C - множество символов, обозначающих константы;
2. V - множество символов, обозначающих переменные;
3. F - множество функциональных символов,
   
   , где
   
   - множество символов для обозначения функций k переменных.

Вводя различные множества символов, мы постоянно обращаемся к их интерпретации ("... символы, обозначающие..."). Строго говоря, это не нужно - можно (а с чисто формальной точки зрения - и должно) описать все правила действия с символами, не прибегая к их интерпретации, однако ее использование позволяет сократить изложение формальных правил за счет обращения к имеющемуся содержательному опыту.

Термы определяются индуктивно:

1. любой символ из
   
   есть терм;
2. если
   
   - термы и
   
   , то
   
   - терм.

Множество термов T представляет собой объединение:

где

,

Удобно разбить T на непересекающиеся множества - слои

. Элементы будем называть термами глубины i или i-слойными термами. Множеству принадлежат выражения, обозначающие те функции от термов предыдущих слоев , которые сами им не принадлежат1).

Для оперирования с термами очень полезны две теоремы [3.4].

Эта теорема является точной формулировкой эквивалентности используемой бесскобочной и обычной записи.

Пусть u и v - выражения, то есть последовательности символов алфавита. Скажем, что u входит в v, если существуют такие выражения p и q (возможно, пустые), что v совпадает с puq.

Теорема 2 (о вхождении терма в терм). Пусть , - термы, t представляется в виде , ? - терм и ? входит в t. Тогда или ? совпадает с t, или ? входит в одно из .

Доказываются эти теоремы элементарной индукцией по длине термов [3.4]. В доказательстве теоремы 2 выделяется лемма, представляющая и самостоятельный интерес.

Лемма 1. Каждое вхождение любого символа в терм ? начинает вхождение некоторого терма в ?.

Определим отношение между термами индуктивным образом "сверху вниз" - по глубине вхождения:

1. 
   ;
2. если t совпадает с
   
   ,
   
   и
   
   - термы, то
   
   ;
3. если
   
   и
   
   , то
   
   .

Согласно теореме 2, тогда и только тогда, когда входит в .

Для каждого терма t определим множество входящих в него термов . Если , то при непусты множества . При этом множество состоит из одного элемента - исходного терма t.

Свяжем с термом t ориентированный граф с вершинами, взаимнооднозначно соответствующими термам из . Будем одинаково обозначать вершины и соответствующие им термы. Пара вершин образует ориентированное от к ребро графа , если терм имеет вид , , - термы и один из них совпадает с . Вершины графа удобно располагать по слоям .

Для произвольного графа G будем обозначать v(G) множество вершин, а e(G) - множество ребер G.

Возьмем для примера выражение для сложной функции

(3)

В принятой выше бесскобочной префиксной записи оно имеет вид

(3')

где все функциональные символы принадлежат .


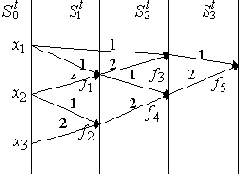
Рис. 3.1. 

Граф для этого терма изображен на рис. 3.1.

Для того, чтобы терм однозначно восстанавливался по графу, необходимы еще два дополнения.

1. Сопоставим каждой вершине
   
   метку p(?) - символ алфавита. Если вершина принадлежит нулевому слою
   
   , то ей соответствует терм, совпадающий с символом из
   
   . Этот символ и сопоставляется вершине в качестве метки.
   
   
   Если вершина принадлежит
   
   (i>0), то меткой служит функциональный символ: вершине ? сопоставляется
   
   , если ? имеет вид
   
   , где
   
   , а
   
   - термы.
2. Каждому ребру
   
   , приходящему в вершину ?, сопоставим метку P(?', ?) - конечное множество натуральных чисел (номеров): пусть терм ? имеет вид
   
   , где
   
   , а
   
   - термы, тогда ребру (?', ?) сопоставляется множество тех i (
   
   ), для которых ?' совпадает с
   
   . На практике в большинстве случаев эта метка состоит из одного номера, но возможны и другие варианты - так же, как функции вида f(x,x). Для графических иллюстраций удобно ребра (?', ?), имеющие в своей метке P(?', ?) больше одного номера, рисовать как пучок ребер, идущих от вершины ?' к вершине ? - по одному такому ребру для каждого номера из P(?', ?); этот номер и будет меткой соответствующего ребра из пучка.

Граф вместе со всеми метками будем обозначать . На рис. 3.1 указаны соответствующие метки для разобранного примера.

Итак, для всякого терма t построен ориентированный граф и две функции: первая сопоставляет каждой вершине символ алфавита , вторая (обозначим ее P) - каждому ребру - конечное множество натуральных чисел P(?', ?). Отмеченный граф - набор () обозначаем . Функции p и P удовлетворяют следующему ограничению:

А) если для данного множество входящих ребер (?', ?) непусто, то (является k-местным функциональным символом при некотором k) и семейство множеств

при фиксированном ? образует разбиение множества номеров {1,...,k}, то есть



при ,



На этом завершается изложение основных формальных конструкций. Прежде, чем переходить к интерпретации, сформулируем теорему об эквивалентности графического и формульного представления термов.

Пусть G - конечный ориентированный граф, не имеющий ориентированных циклов, и в G существует и единственна такая вершина , к которой от любой вершины ведет ориентированный путь. Пусть, далее, заданы две функции: p - на множестве вершин G со значениями в множестве символов алфавита и P - на множестве ребер G со значениями в множестве конечных наборов натуральных чисел и выполнено условие A.



Теорема 3. Существует и единственен терм t, для которого .

Доказательство проводится в два этапа. Сначала в G устанавливается послойная структура: строится разбиение множества вершин G: . Множество состоит из тех вершин, к которым не ведет ни одного ребра - из-за отсутствия ориентированных циклов такие вершины существуют. Множество состоит из тех вершин, к которым ведут ребра только из элементов . Последний непустой элемент в последовательности состоит из одной вершины , все предшествующие элементы этой последовательности непусты, а объединение всех содержит все вершины G.

Доказательство основного утверждения теоремы проводится индукцией по числу слоев k.

Интерпретация сопоставляет терму сложную функцию. Она строится так. Задается некоторое множество D - область интерпретации. Каждой константе с, входящей в интерпретируемый терм t, сопоставляется элемент из D (), каждому k-местному функциональному символу f, входящему в t, сопоставляется функция k переменных (мы сохраняем одинаковое обозначение для символов и их интерпретации, это вполне соответствует интуиции и не должно приводить к путанице). Каждой переменной, входящей в интерпретируемый терм t, сопоставляется переменная, пробегающая D. В результате терму t сопоставляется функция n переменных , где n - число различных символов переменных, входящих в t. Эта "сложная" функция получается суперпозицией "простых" функций, соответствующих функциональным символам.

Если , то есть терм является константой или переменной, то вместо сложной функции получаем константу или тождественную функцию id, переводящую значение переменной в него же. Если , то соответствующая функция является "простой". Истинные сложные функции появляются, начиная со слоя .

Заметим, что заданная интерпретация терма t одновременно определяет интерпретацию каждого терма, входящего в t.

Представим процесс вычисления сложной функции с помощью отмеченного графа . Строится два представления: статическое (все результаты промежуточных вычислений располагаются на графе) и динамическое (шаг за шагом, слой за слоем).





Пусть задана интерпретация терма t и определены значения всех переменных, входящих в t. Тогда для любого терма ?, входящего в t, также задана интерпретация и определены значения всех функций . Каждой вершине ?, входящей в граф , сопоставляется значение функции - элемент D. При этом вершинам нулевого слоя соответствуют значения переменных и констант, а единственной вершине последнего (выходного) слоя - значение . Будем называть элементы D, соответствующие вершинам, значениями этих вершин и обозначать их Z(? ).

Для каждой вершины ?, принадлежащей ненулевому слою, можно выписать уравнение функционирования, связывающее значения вершин. Пусть , и in(?) - совокупность входящих в ? ребер. Напомним, что совокупность меток ребер, оканчивающихся в ?,



образует разбиение множества {1,2,...,k}.

Уравнение функционирования для вершины ?, принадлежащей ненулевому слою, имеет вид

(4)

при

В силу уравнения функционирования (4), если для входящих в ? ребер известны значения Z(?') и задана интерпретация символа - метки вершины, то можно найти значение вершины Z(?). На основании этого (очевидного) замечания строится динамическое представление вычисления сложной функции.

С каждой вершиной графа ?, принадлежащей ненулевому слою, ассоциируется автомат, вычисляющий функцию , где - метка вершины ?. Автоматы срабатывают по слоям в дискретные моменты времени (такты) - автоматы i-го слоя в i-й момент времени. В начальный момент сформированы значения вершин нулевого слоя - известны значения переменных и констант. Они поступают на входы автоматов первого слоя в соответствии с нумерацией аргументов. После i-го такта функционирования определены значения вершин, принадлежащих слоям . На i+1-м такте автоматы i+1-го слоя вычисляют значения вершин i+1-го слоя, получая входные сигналы с предыдущих слоев по правилу (4) - в соответствии с метками входящих ребер.


Содержание раздела

---

---