Сокращение "твердого" объекта

Рассмотрим взаимодействие мышцы с тем объектом, к которому она приложена. Сокращаясь, она должна увлекать клетки объекта или только его оболочку, имитируя сокращение не только мышцы, но и всего объекта.

Пусть, как и ранее, задано значение 0

1 , приводящее к сокращению объекта в направлении мышцы АВ (рис. 15.3). Объект должен преобразиться, как показано на рисунке пунктиром. Мышца описывается системой параметрических уравнений (15.1). М, как и прежде, — неподвижная (относительно неподвижного объекта) точка мышцы. Однако эта точка теперь определяет плоскость М, перпендикулярную мышце, относительно которой слева и справа все значащие клетки объекта должны сместиться в направлении к этой плоскости, т.е. параллельно мышце, с коэффициентом смещения (сжатия), равным l.

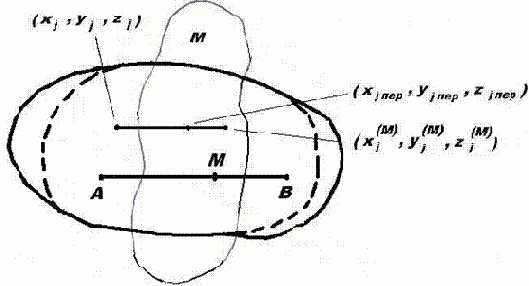
Рис. 15.3. Сокращение твердого тела

Плоскость М описывается уравнением

(15.4)

Пусть точка (xj, yj, zj) — текущая клетка объекта с адресом xjyjzj

, подлежащая указанному переносу. Найдем координаты xj(M), yj(M), zj(M)

ее проекции на плоскость М. Так как точка с этими координатами принадлежит плоскости М и минимизирует квадрат расстояния точки (xj, yj, zj) до этой плоскости, задача такой условной минимизации формулируется так:

найти значение xj(M), yj(M), zj(M)

, удовлетворяющее требованию

(xj(M) - xj )2

+ (yj(M) - yj)2 + (zj(M)

- zj)2

min

при условии

(xj(M) - xM)(x1

- xM) + (yj(M) - yM)(y1

- yM) + (zj(M) - zM)(z1

- zM) = 0.

Решим данную задачу, используя уравнение Лагранжа

(xj(M) - xj)2

+ (yj(M) - yj)2 + (zj(M) - zj)2 + ?[(xj(M)

- xM)(x1 - xM) + (yj(M) - yM)(y1

- yM) + (zj(M) - zM)(z1 - zM)]

min.

Дифференцируя по всем переменным, включая ?, и приравнивая производные нулю, получим систему линейных уравнений

2(xj(M) - xj) + ?(x1 - xM) = 0

2(yj(M) - yj) + ?(y1 - yM) = 0

2(zj(M) - zj) + ?(z1 - zM) = 0

(xj(M) - xM)(x1 - xM) + (yj(M) - yM)(y1 - yM) + (zj(M) - zM)(z1 - zM) = 0.

Решая систему, находим

(15.5)

Таким образом, получена мышца с началом в точке (клетке) с координатами xj, yj, zj

и с концом в точке xj(M), yj(M), zj(M)

. Эта же точка является неподвижной. Тогда по (14.2) и (14.3) имитируется сжатие мышцы. Цикл по j охватывает все значащие клетки объекта.

Содержание раздела