Шарнирно-мышечное соединение

Координаты шарнира задаются условно (ячейка не занимается) точкой O(x0, y0, z0) внутри объекта (рис. 15.6). Мышца АВ связывает лучи (элементы скелета), исходящие из точки О. Сокращение мышцы должно вызывать видимость движений, характерных при ходьбе, движении рук и т.д. Это требует таких деформаций объектов, при которых его клетки, облегающие эти лучи, или только клетки оболочки, несущие в себе данные лучи, сближаются вместе с лучами, не приводя к дополнительной деформации.

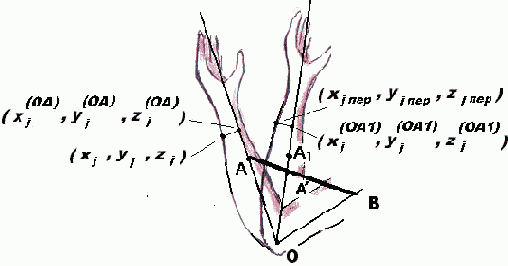
Рис. 15.6. Деформация объекта вокруг шарнира

Практический интерес представляет случай, когда неподвижная точка мышцы совпадает с одним из ее концов. Это соответствует направлению движения конечности относительно неподвижного тела. (Хотя следование известным соотношениям о количестве движения или третьего закона механики не представляет трудностей.)

По аналогии с (15.1), луч ОА описывается параметрической системой уравнений

(15.12)

Если 0

1, то уравнения отображают отрезок ОА. Нас же интересует вся прямая, исходящая из точки О.

Отобразим сокращение мышцы переносом клетки А в клетку А' (x1', y1', z1' ), в упрощенной форме воспользовавшись (15.2) и (15.3). Этим установим новое положение ОА'луча ОА.

Уравнения этого луча имеют вид

(15.13)

Если 0

1, то уравнения отображают отрезок ОА'. Однако точка А' не отображает факт вращения луча ОА вокруг точки О. При этом вращении точка А должна переместиться в точку А1

, отстоящую от О на расстояние, равное длине отрезка ОА. Найдем координаты этой точки на луче ОА' из соотношения

(x11 - x0)2

+ (y11 - y0)2 + (z11

- z0)2 = r2 = (x1 - x0)2

+ (y1 - y0)2 + (z1 - z0)2.

В параметрической форме представления (12) точке (x11, y11, z11) соответствует некоторое значение k1' параметра. Подставим вместо координат этой точки их параметрическое представление:

(k1')2((x1' - x0)2 + (y1' - y0

)2 + (z1' - z0)2) = r2

Откуда

(15.14)

Очевидно, k1' > 0 . Таким образом, точка А1

переноса конца А мышцы найдена.

Для синхронных действий при переносе всех клеток объекта, подлежащих перемещению вокруг шарнира, запишем уравнения луча ОА1

в зависимости от того же параметра k, определяющего положение (15.12) луча ОА

(15.15)

Пусть (xj, yj, zj) — точка (клетка), подлежащая переносу, в соответствии с сокращением мышцы, в точку с тем же радиусом относительно точки О, но с исключением других деформаций объекта. Чтобы найти координаты (xj(OA), yj(OA), zj(OA)) проекции этой точки на луч ОА, решим задачу минимизации расстояния между этой точкой и лучом ОА, описанным системой (15.12):

(xj - k(x1 - x0)- x0)2 + (yj - k(y1 - y0) - y0)2 + (zj - k(z1 - z0) - z0)2

min.

Приравняв производную по k нулю, получим

(xj - k(x1 - x0) - x0)(x1 - x0) + (yj - k(y1 - y0) - y0 )(y1 - y0) + (zj - k(z1 - z0) - z0)(z1 - z0) = 0.

Отсюда

(15.16)

Подставим (15.16) в (15.12) и найдем координаты (xj(OA), yj(OA), zj(OA)) искомой проекции.

Вычислим разности координат точки (xj, yj, zj) и найденной ее проекции на луч ОА, определяющие смещение этой точки:

(15.17)

Подстановкой (15.15) в (15.14) найдем координаты (xj(OA1), yjOA1), zj(OA1)) "образа" точки (xj(OA), yjOA), zj(OA))

при повороте луча. Тогда координаты x

j пер , yj пер, zj пер

переноса точки (xj, yj, zj) отыскиваются так:

(15.18)

Организовав цикл по j - по всем точкам объекта (или оболочки) в окрестности луча ОА, выполним требуемую имитацию движения.

Содержание раздела