Возможность применения однослойных нейросетей
Исследуем передаточную функцию 3 и использующую ее нейросеть на рис. 10.2. Анализируя прохождение сигнала по нейросети при предъявлении s-й эталонной ситуации, т.е. подавая на вход соответствующую комбинацию ns единиц, видим, что при единичных весах связей нейронов выходного слоя значение возбуждения нейрона, соответствующего решению, равно ns. Эта величина не зависит от пути прохождения возбуждения каждого рецептора, т.е. от того, сколько нейронов было на его пути. Сказывается свойство ассоциативности выбранной передаточной функции при малом значении порога. В этом случае свойство ассоциативности вырождается в свойство аддитивности, где функция от набора значений равна сумме функций от каждого значения.
Действительно, комбинация Х1 = Х3 = Х5 = Х7 = 1 приводит к величине возбуждения нейрона R1 , равной 4, значение Х10 = 1 приводит к единичному возбуждению того же нейрона, комбинация Х1 = Х6 = Х7 = 1 приводит к величине возбуждения нейрона R2 , равной 3, и т.д.
Возникает вопрос: не проще ли сформировать нейросеть, приблизив ее к табличному виду с помощью связей, непосредственно соединяющих множество тех рецепторов, которые образуют ситуации, приводящие к одному решению, с нейроном, закрепленным за этим решением?
Итак, создавая нейросеть на основе логической схемы обработки высказываний, мы заменили операции


 |
(10.3) |
Множество всех высказываний или соответствующих им рецепторов, участвующих в формировании одного решения, в лекции 3 была названа обобщенной ситуацией.
Множество {X1 , X3 , X5 , X10 } является обобщенной ситуацией, аналогично – множество {X1 , X2 , X4 , X6 , X7 , X12 , X14 } и т.д.
В сущности, это не означает, что при формировании каждого решения все нейроны-рецепторы, образующие обобщенную ситуацию, должны получать ненулевое возбуждение.
Она делит подмножество на два, каждое из которых содержит единственный элемент. Закрепляем за ними (окончательно, за соответствующими связями) значение веса 0,25, т.е. ранее найденное значение 0,5 делим поровну (рис. 10.3).
Анализ следующего подмножества приводит к аналогичному результату. Последнее подмножество содержит два элемента, объединенных в (10.2) операцией конъюнкции. За каждым из них окончательно закрепим вес связи, равный 0,5.
Рассмотрим следующую логическую функцию, приводящую к решению R2. Здесь последняя производимая операция – дизъюнкция. Она делит множество нейронов, составляющих обобщенную ситуацию, на два подмножества: {X1, X7, X4, X6} и {X2, X12, X14}. Присвоим им предварительно единичные веса связей.
Анализируя первое подмножество, находим последнюю логическую операцию – конъюнкцию, разделяющую его на два меньших подмножества {X1, X7} и {X4, X6}. Введенный ранее единичный вес делим поровну, принимая уточненные веса связей нейронов равными 0,5.
Вновь анализируем первое из сформированных множеств нейронов. Операция конъюнкции делит это подмножество на два, содержащие по одному элементу: {X1} и {X7}. Делим поровну найденный ранее вес, полагая веса соответствующих связей нейрона R2 равными 0,25.
Последней логической операцией, связывающей высказывания Х4 и Х6 второго подмножества, является дизъюнкция. Она окончательно сохраняет ранее определенный вес связей, равный 0,5.
Анализируя третье, последнее подмножество, видим, что в записи, объединяющей высказывания в (10.2), отсутствуют скобки. Это (хотя существует ранжирование логических операций при их выполнении) свидетельствует о том, что все высказывания объединяет одна операция. Так как это – конъюнкция, делим поровну предварительно найденный вес, полагая соответствующие веса связей равными 0,33.
Аналогично корректируем остальные веса связей.
Рассмотрение примера приводит к простому формальному описанию алгоритма коррекции весов связей нейронов выходного слоя однослойной нейросети, которое здесь не приводим.
В табл. 10. 3 даны результаты расчета ситуаций, отображенных в табл. 10.1 и 10.2.
Видим, что по эталонным ситуациям нейросеть "работает" правильно, что порождает доверие к ней в процессе эксплуатации. Вполне объяснимы и другие решения, совпадающие с ранее полученными.
Рассуждения об ассоциативности передаточной функции приводят к предположению о полном совпадении результатов расчетов возбуждения нейронов выходного слоя, отображенных в табл. 10.2 и табл. 10.3. Однако это не так. А именно: нахождение весов связей внесло коррективы, и результаты расчетов несущественно отличаются. Несущественность этого несовпадения определяется тем, что, во-первых, для всех эталонов совпадают принимаемые решения, во-вторых – для одинаковых ситуаций сохраняется предпочтительный ряд таких решений.
| 0 | 0 | 0 | 0,5 | 0 | 0 | 1 | 0,55 | 0,95 | 0,25 |
| 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 1 | 0,5 | 0,55 | 0,8 | 0,65 |
| 0,5 | 0,5 | 0,5 | 0 | 1 | 0,5 | 0 | 0,55 | 0,05 | 0,4 |
| 0,5 | 1 | 1 | 1 | 0 | 0,25 | 0,25 | 1,16 | 0,33 | 1,54 |
| 1 | 0,5 | 0,5 | 0 | 0,5 | 0,25 | 0,5 | 0,78 | 0,33 | 0,45 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0,6 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0,6 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0,4 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0,1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0,3 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0,1 | 0 | 0,3 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0,9 | 0 | 0,3 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0,5 | 0 | 0,5 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0,5 | 0 | 0,5 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0,2 | 0 | 0,5 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0,8 | 0 | 0,5 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0,1 | 0,9 | 0,5 |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0,9 | 0,1 | 0,5 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Обобщенные ситуации имеют "технологическое" значение. Они объединяют нейроны-рецепторы, между которыми, с одной стороны, и нейроном выходного слоя – с другой должны быть введены связи в однослойной нейросети. Нейроны-рецепторы по-прежнему возбуждаются в соответствии с ситуациями – конъюнкциями высказываний, для которых формируется нейросеть. А оператор нейросети следит за тем, чтобы "физический смысл" явлений не пропадал, а именно – чтобы соблюдались права исчерпывающих множеств событий.
По описанию (10.3) построим однослойную нейросеть (рис. 10.3, на веса пока не обращаем внимания) и проанализируем ее работу при ситуациях, отображенных в таблицах 10.1 и 10.2.
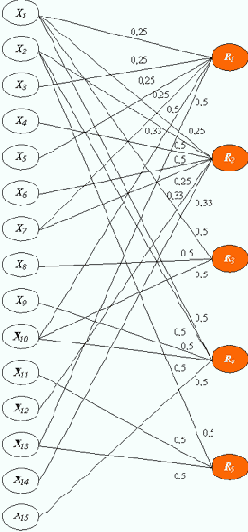
Рис. 10.3. Однослойная нейросеть
Видим, что нейросеть в целом делает верные выводы. Взаимно-относительные оценки возбуждения нейронов выходного слоя правильно определяют ситуации, однако абсолютные значения возбуждения этих нейронов различны для различных ситуаций. Тогда, как и прежде, приведем их к отрезку [0, 1], скорректировав веса связей. Для воспроизведения структуры и взаимодействия высказываний и ситуаций придется обратиться к описанию (10.2). Определим по первой логической функции в (10.2), задающей решение R1, последнюю операцию. Это операция дизъюнкции.
Она делит множество нейронов обобщенной ситуации на два подмножества {X1, X3, X5, X7} и {X10, X13}. Закрепим предварительно за ними единичное значение весов связей.
В этом разбиении на непересекающиеся подмножества нам помогает отмеченная ранее единственность вхождения каждого выражения в запись логической функции.
Отдельно исследуем сформированные подмножества.
По первому из них находим последнюю выполняемую логическую операцию. Это операция конъюнкции, разбивающая подмножество на два меньших: {X1, X7} и {X3, X5}. Закрепим за каждым из них значение веса 0,5 (ранее найденную единицу делим поровну).
Вновь, начиная с первого, анализируем последовательность трех подмножеств. Последняя операция, производимая над элементами первого подмножества, является конъюнкцией.
Она делит подмножество на два, каждое из которых содержит единственный элемент. Закрепляем за ними (окончательно, за соответствующими связями) значение веса 0,25, т.е. ранее найденное значение 0,5 делим поровну (рис. 10.3).
Анализ следующего подмножества приводит к аналогичному результату. Последнее подмножество содержит два элемента, объединенных в (10.2) операцией конъюнкции. За каждым из них окончательно закрепим вес связи, равный 0,5.
Рассмотрим следующую логическую функцию, приводящую к решению R2. Здесь последняя производимая операция – дизъюнкция. Она делит множество нейронов, составляющих обобщенную ситуацию, на два подмножества: {X1, X7, X4, X6} и {X2, X12, X14}. Присвоим им предварительно единичные веса связей.
Анализируя первое подмножество, находим последнюю логическую операцию – конъюнкцию, разделяющую его на два меньших подмножества {X1, X7} и {X4, X6}. Введенный ранее единичный вес делим поровну, принимая уточненные веса связей нейронов равными 0,5.
Вновь анализируем первое из сформированных множеств нейронов. Операция конъюнкции делит это подмножество на два, содержащие по одному элементу: {X1} и {X7}. Делим поровну найденный ранее вес, полагая веса соответствующих связей нейрона R2 равными 0,25.
Последней логической операцией, связывающей высказывания Х4 и Х6 второго подмножества, является дизъюнкция. Она окончательно сохраняет ранее определенный вес связей, равный 0,5.
Анализируя третье, последнее подмножество, видим, что в записи, объединяющей высказывания в (10.2), отсутствуют скобки. Это (хотя существует ранжирование логических операций при их выполнении) свидетельствует о том, что все высказывания объединяет одна операция. Так как это – конъюнкция, делим поровну предварительно найденный вес, полагая соответствующие веса связей равными 0,33.
Аналогично корректируем остальные веса связей.
Рассмотрение примера приводит к простому формальному описанию алгоритма коррекции весов связей нейронов выходного слоя однослойной нейросети, которое здесь не приводим.
В табл. 10. 3 даны результаты расчета ситуаций, отображенных в табл. 10.1 и 10.2.
Видим, что по эталонным ситуациям нейросеть "работает" правильно, что порождает доверие к ней в процессе эксплуатации. Вполне объяснимы и другие решения, совпадающие с ранее полученными.
Рассуждения об ассоциативности передаточной функции приводят к предположению о полном совпадении результатов расчетов возбуждения нейронов выходного слоя, отображенных в табл. 10.2 и табл. 10.3. Однако это не так. А именно: нахождение весов связей внесло коррективы, и результаты расчетов несущественно отличаются. Несущественность этого несовпадения определяется тем, что, во-первых, для всех эталонов совпадают принимаемые решения, во-вторых – для одинаковых ситуаций сохраняется предпочтительный ряд таких решений.
| 0 | 0 | 0 | 0,5 | 0 | 0 | 1 | 0,55 | 0,95 | 0,25 |
| 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 1 | 0,5 | 0,55 | 0,8 | 0,65 |
| 0,5 | 0,5 | 0,5 | 0 | 1 | 0,5 | 0 | 0,55 | 0,05 | 0,4 |
| 0,5 | 1 | 1 | 1 | 0 | 0,25 | 0,25 | 1,16 | 0,33 | 1,54 |
| 1 | 0,5 | 0,5 | 0 | 0,5 | 0,25 | 0,5 | 0,78 | 0,33 | 0,45 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0,6 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0,6 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0,4 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0,1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0,3 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0,1 | 0 | 0,3 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0,9 | 0 | 0,3 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0,5 | 0 | 0,5 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0,5 | 0 | 0,5 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0,2 | 0 | 0,5 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0,8 | 0 | 0,5 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0,1 | 0,9 | 0,5 |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0,9 | 0,1 | 0,5 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Однако всегда ли можно так упростить задачу создания СПР, сведя ее к получению однослойной нейросети? В разделе 9.1 показано, что это не всегда возможно. Там приведена попытка воспроизведения логического описания СПР
 | (10.4) |
Однако дело не столь безнадежно. Рассмотрим обобщенные эталоны, определяющие каждое решение:
 | (10.5) |
Изменим логическое описание, "размножив" одинаковые решения так, чтобы ни один обобщенный эталон не оказался включенным в другой. Для этого введем условно два одинаковых решения R11 = R12 = R1.
Представим систему (9.6) в виде
 | (10.6) |
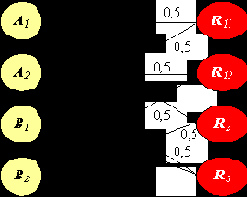
Рис. 10.4. Нейросеть, построенная по описанию (10.6)
Легко видеть, что в ней отсутствует побочный эффект, т.е. корректировка порогов не требуется.
Таким образом, для применения однослойных нейросетей необходимо (достаточно ли?), чтобы обобщенная ситуация, соответствующая одному решению, не поглощала все нейроны, которые образуют некоторую ситуацию, ведущую к другому решению.
Так, если не была бы найдена логическая ошибка, в результате чего ситуация Х10 в (9.1) не сменилась ситуацией Х10

в (10.1)-(10.2), обобщенные ситуации, ведущие к решениям R3 и R4, поглотили бы эту ситуацию. Это значит, что при задании эталона Х8 = Х10 = 1 единичное значение возбуждения получали бы нейроны R1 и R3. Аналогично, предъявление эталона Х9 = Х10 = 1 привело бы к единичному значению возбуждения нейронов R1 и R4.