Корректировка весов связей нейронов выходного

ДНФ наглядно демонстрирует смысл задачи, так как каждая конъюнкция, включая содержащую единственное высказывание, соответствует отдельной ситуации. Дизъюнкция таких конъюнкций определяет множество ситуаций, приводящих к одному решению. Отсюда, прообразами нейронов выходного слоя являются дизъюнкторы, реализующие операцию ИСКЛЮЧАЮЩЕЕ ИЛИ, т.е. предполагающие анализ не более чем одного единичного сигнала на входе.

Выше было установлено, что при замене логических операций счетом единой передаточной функции даже для эталонных ситуаций возможен побочный эффект, при котором на один нейрон выходного слоя для совместной обработки поступают высокие сигналы возбуждения более чем одного нейрона, т.е. отображающие одновременное наличие разных ситуаций. Это способствует неоднозначности решений.

Показано, что с помощью порогов можно ликвидировать побочный эффект, и мы вправе считать, что высокий сигнал возбуждения, соответствующий действительной ситуации, воспринимается нейроном выходного слоя с единственного входа, что в большей степени адекватно имитируемой логической операции.

Однако величина возбуждения нейронов выходного слоя осталась различной в связи с различной величиной возбуждения нейронов скрытого (промежуточного) слоя.

Введем веса связей (входов) каждого нейрона выходного слоя, равные обратной величине уровня сигнала при предъявлении эталонной ситуации, поступающего на каждый вход. Этим мы добьемся принадлежности величин возбуждения нейронов выходного слоя диапазону [0, 1]. Этот диапазон будет реализован при "грамотном" задании достоверности событий на рецепторном входе.

Выбранный диапазон уравнивает роль входного и выходного слоев в случае, если при создании "длинных" логических цепочек умозаключений реализуется вложенность нейросетей. Это означает, что выходной слой одной нейросети тотчас используется в качестве входного слоя другой.

В исследуемом примере веса связей вводятся на основе анализа величин возбуждения нейронов выходного слоя при рассмотрении всех возможных эталонов, как представленных в табл. 9.1, так и немногих оставшихся.
Полученные веса отображены на рис. 9.15.

Однако после корректировки весов, приведшей к одинаковому, единичному значению возбуждения нейронов выходного слоя в ответ на каждую эталонную ситуацию, вновь замечаем возникшую неоднозначность решения. А именно, высказывание Х10 образует эталонную ситуацию, приводящую к решению R1. В то же время Х10 участвует в создании ситуаций Х8

Х10

и Х9

Х10, приводящих к решениям R3 и R4 соответственно. То есть задание эталона Х8 = Х10 = 1 приводит в единичное возбуждение нейроны R1 и R3, а задание Х9 = Х10 = 1 порождает значения R1 = R4 = 1.

Исследуя пути исправления ошибки, приходим к выводу, что в основе обнаруженной коллизии лежит некорректное описание СПР, необнаруженное противоречие в задании на разработку. Еще на этапе составления логической схемы (рис. 9.15) мы могли обнаружить получение единичных сигналов не на единственном выходе.

Тогда вспоминаем, что бесплатный билет – проездной документ – предъявляется обязательно вместе с удостоверением работника МПС!

Дополним описание (9.1), уточнив логическое выражение для R1:

(10.1)

Появление новой конъюнкции высказываний приводит к увеличению числа нейронов промежуточного слоя (рис. 10.1), т.к. вместо связи X1

R1 вводится нейрон 12. Порог h12 = 1,4. Вес связи нейрона 12 с нейроном R1 принимает значение 0,5.

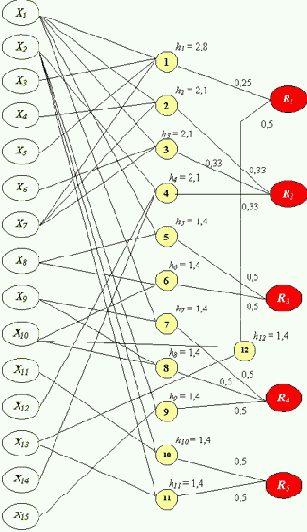
Рис. 10.1. Нейросеть после уточнения логического описания

В табл. 10.1 представлены результаты расчета принимаемых решений по предъявленным эталонным ситуациям (для проверки правильности) и по ряду неопределенных ситуаций (столбцы 8-10). Анализ таблицы показывает, что решения, принятые нейросетью, вполне объяснимы. Это относится даже к неоднозначному решению (столбец 9).

Таблица 10.1. Расчет принимаемых решений по уточненной нейросети после корректировки порогов и весов связейРешениеR1R2R2R2R3R4R5R1R4R5R2Возбуждение нейронов выходного слоя R5R4R3R2R1Возбуждение нейронов промежуточного слоя121110987654321СитуацияX15X14X13X12X11X10X9X8X7X6X5X4X3X2X1№

0	0	0	0	0	0	1	0	0,75	0
0	0	0	0	0	1	0	0	0,75	0
0	0	0	0	1	0	0	0	0	0
0	1	1	1	0	0	0	0,77	0	0,83
1	0	0	0	0	0	0	0,87	0	0
0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	2	0	1,5	0
0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	1,5	0
0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	2	0	0	0	0
0	0	0	0	2	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0
0	0	0	3	0	0	0	0	0	2,5
0	0	3	0	0	0	0	2,3	0	0
0	3	0	0	0	0	0	0	0	0
4	0	0	0	0	0	0	3,1	0	0
0	0	0	0	0	0	0	0	0,6	0
0	0	0	1	0	0	0	1	0	1
0	0	0	0	0	0	1	0	0,6	0
0	0	0	1	0	0	0	0	0	1
0	0	0	0	0	0	0	1	0,4	0
0	0	0	0	1	0	0	0,1	0	0
0	0	0	0	0	1	0	0	0	0,3
0	0	0	0	1	0	0	0,1	0	0,3
1	1	1	0	0	0	0	0,9	0	0,3
0	0	1	0	0	0	0	0,5	0	0,5
1	0	0	0	0	0	0	0,5	0	0,5
0	1	0	0	0	0	0	0,2	0	0,5
1	0	0	0	0	0	0	0,8	0	0,5
0	0	0	1	0	0	1	0,1	0,9	0,5
1	1	1	0	0	1	0	0,9	0,1	0,5
1	2	3	4	5	6	7	8	9	10

Полученные веса отображены на рис. 9.15.

Однако после корректировки весов, приведшей к одинаковому, единичному значению возбуждения нейронов выходного слоя в ответ на каждую эталонную ситуацию, вновь замечаем возникшую неоднозначность решения. А именно, высказывание Х10 образует эталонную ситуацию, приводящую к решению R1. В то же время Х10 участвует в создании ситуаций Х8

Х10

и Х9

(10.1)

R1 вводится нейрон 12. Порог h12 = 1,4. Вес связи нейрона 12 с нейроном R1 принимает значение 0,5.

0	0	0	0	0	0	1	0	0,75	0
0	0	0	0	0	1	0	0	0,75	0
0	0	0	0	1	0	0	0	0	0
0	1	1	1	0	0	0	0,77	0	0,83
1	0	0	0	0	0	0	0,87	0	0
0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	2	0	1,5	0
0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	1,5	0
0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	2	0	0	0	0
0	0	0	0	2	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0
0	0	0	3	0	0	0	0	0	2,5
0	0	3	0	0	0	0	2,3	0	0
0	3	0	0	0	0	0	0	0	0
4	0	0	0	0	0	0	3,1	0	0
0	0	0	0	0	0	0	0	0,6	0
0	0	0	1	0	0	0	1	0	1
0	0	0	0	0	0	1	0	0,6	0
0	0	0	1	0	0	0	0	0	1
0	0	0	0	0	0	0	1	0,4	0
0	0	0	0	1	0	0	0,1	0	0
0	0	0	0	0	1	0	0	0	0,3
0	0	0	0	1	0	0	0,1	0	0,3
1	1	1	0	0	0	0	0,9	0	0,3
0	0	1	0	0	0	0	0,5	0	0,5
1	0	0	0	0	0	0	0,5	0	0,5
0	1	0	0	0	0	0	0,2	0	0,5
1	0	0	0	0	0	0	0,8	0	0,5
0	0	0	1	0	0	1	0,1	0,9	0,5
1	1	1	0	0	1	0	0,9	0,1	0,5
1	2	3	4	5	6	7	8	9	10

Содержание раздела