Нейросеть произвольной структуры
Предположим, мы располагаем некоторым банком "красиво" изображенных графических схем, которые можно положить в основу структуры нейросети. Понравившуюся структуру мы решаем интерпретировать как нейросеть, дополнив ее передаточной функцией и обучив решению задачи, поставленной дядей Рамзаем.
Пусть выбранная нами нейросеть имеет 12 входов (более чем достаточно), 5 выходов и реализует ту же передаточную функцию с начальными значениями весов ?ij = 0 и порога h = 0.
Однако сеть обладает специфической топологией, затрудняющей ее обучение. Сеть многослойная, что исключает связи "через слой", присутствующие, например, на рис. 3.7 как результат построения нейросети "под задачу". Да и связь между слоями скорее соответствует известному предупреждению "шаг влево, шаг вправо…".
Будем использовать метод опорных путей, или трассировки, расширяющий использованный выше "схемотехнический" подход. Его можно изобразить схемой рис. 3.2



Итак, для успешной, наглядной и легко рассчитываемой трассировки решим вопрос кардинально: какие веса полагать равными нулю, а какие - единице? Все прочие возможности, например min ?ij = 0,1, введение порога h = 0,5 и т.д., будут способствовать более плавной работе сети, непрерывности перехода из состояния в состояние.
Применив принципы комбинаторики и эвристики, выполним трассировку нейросети (рис. 3.13). На рисунке наглядно показано, какая нейросеть была предоставлена, насколько она "неповоротлива", скажем, по сравнению с однослойной "каждый с каждым".
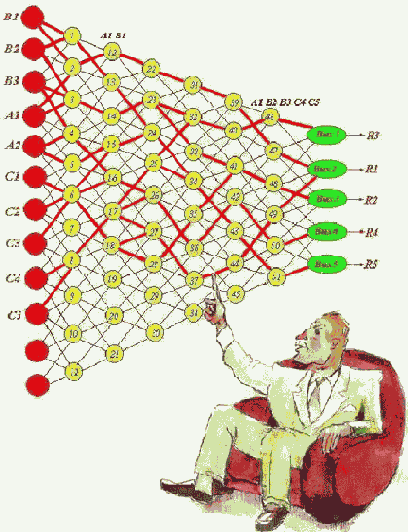
Рис. 3.13. Результат трассировки многослойной нейросети
Далее будет представлен формальный алгоритм трассировки. Однако чтобы настроиться на его понимание, следует проанализировать свои действия и сделать следующие выводы:
- Мы анализировали слой за слоем, постоянно помня цель - пять комбинаций ситуаций, каждая из которых должна возбудить один из нейронов выходного слоя, не вводя пока жесткое закрепление решений за этими нейронами.
- В каждом слое мы собирали частную комбинацию - терм, который можно использовать в последующем, - из доступных термов предыдущего слоя.
- Термы, которые пока не могут быть использованы при конструировании из-за их взаимной удаленности, мы запоминали без изменения на анализируемом слое, пытаясь их "подтянуть" в направлении возможного дальнейшего объединения.
- Мы старались не "тянуть" термы "поперек" всей сети. В противном случае мы сталкивались бы с проблемой: как избегать пересечений и искажения уже сформированных термов. Все это заставило нас долго не закреплять нейроны выходного слоя за решениями, что в конце концов привело к нарушению естественного порядка следования решений.
Для автоматизации трассировки необходимо матричное представление, только и доступное компьютеру.
Матрица следования, отражающая трассировку нейросети, получается на основе рис. 3.13, если отметить элементы, соответствующие "тонким" линиям, нулевыми весами, а элементы, соответствующие "жирным" линиям, - весами, равными единице.
На рис. 3.14 отражен динамический путь возбуждения, приводящий к решению R1. Он строится по алгоритму, изложенному в разд. 3.5. В данном случае динамические пути возбуждения совпадают со статическими. В общем случае из статического пути возбуждения необходимо исключить нейроны, которые не входят во входной слой и которым соответствуют нулевые строки сформированной матрицы следования.
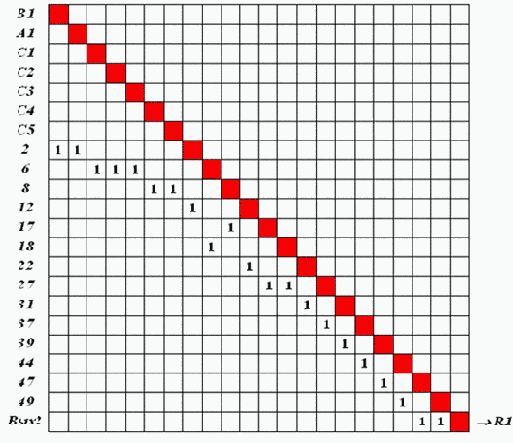
Рис. 3.14. Динамический путь возбуждения
Аналогично получают динамические пути возбуждения, приводящие к другим решениям.
Поставим теперь задачу дальнейших исследований: как построить все необходимые пути возбуждения так, чтобы они, возможно, пересекались, - но только для формирования общих термов? А способна ли выбранная нами "готовая" нейросеть вообще справиться с поставленной задачей или предпочтительнее принцип "нейросеть под задачу"?
…Вот теперь-то мы довольны! Мы снабдили дядю Рамзая универсальной обучаемой нейросетью. Теперь, если он, раскаявшись, вновь возлюбит свою благороднейшую профессию, он найдет ей (сети) достойное применение в водворении Васи, Пети & K0 на то спальное место, которого они действительно заслуживают.