Минимизация длины логической цепочки в системе принятия решений
Предваряя подробное исследование в последующих лекциях, отметим, что замена логических операций операцией суммирования при счете передаточной функции приводит к актуальности однократного учета всех входящих переменных, т.е. к единственности вхождения переменных в каждое логическое выражение, составляющее описание системы принятия решений. Выше с целью обеспечения такого единственного вхождения переменной был использован прием "размножения" решения R6.
При разработке электронных схем исследуется понятие "длина логической цепочки" - под ней подразумевается максимальное количество электронных элементов, которое должен преодолеть сигнал на входе схемы, пройдя последовательное тактируемое преобразование, чтобы на выходе схемы сформировался сигнал. От этой длины, определяющей время переходного процесса, зависит быстродействие схемы. Поэтому актуальной задачей является минимизация максимальной длины логической цепочки при возможности параллельного выполнения всех таких цепочек (что характерно для прохождения электрического сигнала по схеме).
Очевидно, что в схеме на рис. 1.4 максимальная длина логической цепочки равна двум.
Применим ко всем выражениям (1.17), каждое из которых является или может быть преобразовано в дизъюнкцию конъюнкций, прием "размножения" решений. Теперь (рис. 1.9) схема состоит из цепочек единичной длины. Каждый входной сигнал подвергается обработке только конъюнктором. Так как электронная схема полностью определяет конструкцию системы принятия решений на основе достоверности событий, то можно преобразовать полученную электронную схему в однослойную схему СПР, показанную на том же рисунке.
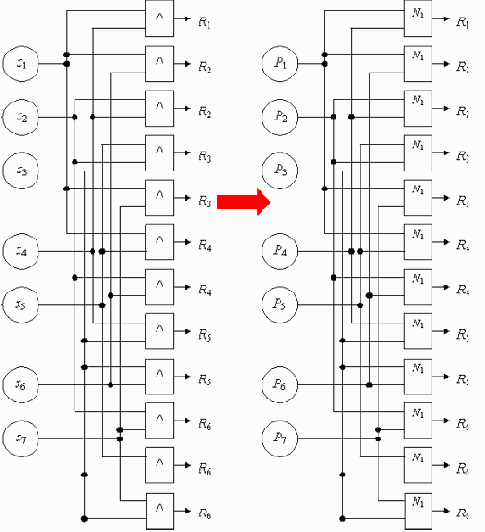
Рис. 1.9. Преобразование электронной схемы с единичной длиной логической цепочки в однослойную систему принятия решений
Таким образом, доказано следующее утверждение:
Лемма 1. Любая СПР, сформированная на основе логического описания булевыми функциями, способом "размножения" решений преобразуется в однослойную СПР на основе достоверности событий.
Преимуществом таких СПР является то, что они представляют собой таблицы с ассоциативной выборкой по принципу наибольшей похожести.
Конечно, можно за каждым решением закреплять один выход СПР, на котором объединить общее решение, полученное по разным путям, в виде текста. При корректно заданных исходных данных - на основе правил использования исчерпывающих множеств событий - СПР будет "работать" правильно, выдавая адекватные ответы. Тогда рекомендация "Прими решение R" будет выдана, а информация о пути, приведшему к этому решению, будет утрачена.
При составлении "электронной" схемы такое объединение производится с помощью операции дизъюнкции, что приводит к длине логической цепочки, равной двум. Но ведь если, формируя структуру СПР, строго следовать порядку построения "электронная схема

Таким образом, "размножение" решений - операция, свойственная СПР, что делает ее (СПР) построение отличающимся, развивающим "схемотехнический" подход. "Электронные" схемы целесообразно использовать на начальном этапе исследования логического описания СПР, а далее, оттолкнувшись от них, перейти к более совершенной однослойной структуре.
"Размножение" решений имеет важное достоинство. Оно позволяет установить причину, найти объяснение принимаемого решения. Это означает, что текст решения может быть дополнен указанием причины принятия именно такого решения.
Например, получив информацию о необходимости заказа велосипеда в отделе спортинвентаря, бабушка может воспользоваться и важным объяснением: "…потому что сейчас, скорее всего, весна, а вы, вероятно, только что сытно позавтракали" (рис. 1.10).

Рис. 1.10. Бабушка
В заключение данной лекции следует отметить, что построен алгоритм параллельных вычислений [6] сложных логических конструкций в области действительных переменных, предназначенный для реализации высокого быстродействия в системах управления и принятия решений.Более того, сведение СПР к однослойной приводит к применению лишь тех передаточных функций (элементов N1 на рис. 1.6 и рис. 1.9), которые имитируют конъюнкторы. Это служит повышению достоверности оценок, стандартизации и адекватности природным процессам.